Sesiones Teóricas Estadística y TIC. Tema 10.

Hipótesis estadísticas. Test de Hipótesis    

Contrastes de hipótesis

Para controlar los errores aleatorios, además del cálculo de intervalos de confianza, contamos con una segunda herramienta en el proceso de inferencia estadística: los test o contrastes de hipótesis à de manera que con los resultados obtengamos podemos rechazar o no la hipótesis nula, es decir, si hay relación o no entre las variables.

Con los intervalos nos hacemos una idea de un parámetro de una población dado un par de números entre los que confiamos que esté el valor desconocido.

Con los contrastes de hipótesis la estrategia es la siguiente:

•      Establecemos a priori una hipótesis cerca del valor del parámetro.
•      Realizamos la recogida de datos
•      Analizamos la coherencia de entre la hipótesis previa y los datos obtenidos

Errores de hipótesis

En este tema estudiamos de nuevo el test de Chi cuadrado, ya explicado anteriormente, dejo aquí un ejemplo para aclararlo de nuevo,

En un C de Salud analizamos las historias de enfermería (292 hombres y 192 mujeres). De ellos tienen úlcera 10 hombres y 24 mujeres y no tienen 282 y 168 respectivamente. Nivel de significación 0, 05. Las hipótesis serías:

– Ho: No existe relación entre tener úlcera y el sexo.

– H1: Sí existe relación entre tener úlcera y el sexo.

Paso 1: Realizar la tabla de las frecuencias observadas y calcular los valores esperados

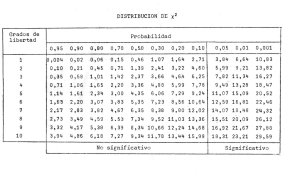
Paso 2: Calcular los grados de libertad.

Grados de libertad = (nº de filas – 1) por (nº de columnas – 1)

Grados de libertad = (2 – 1)(2 – 1) = 1 x 1 = 1

Paso 3: Calcular el valor de chi cuadrado.

Paso 6: Comparar los valores.

– Valor calculado –> 14, 61

– Valor de la tabla –> 3, 84

Conclusión: como 14, 61 > 3, 84, rechazamos Ho y ACEPTAMOS H1. 

Seminario Estadística y TIC. Seminario 5.

Este seminario se dedicó a la exposición de los trabajos de investigación realizado con mis compañeras Lola Monje Ríos y Sara Mejías Segura, aquí os dejo un breve resumen y las conclusiones obtenidas después de un duro trabajo, que no hubiera sido posible sin la ayuda de nuestro profesor Manuel Pavón.

RESUMEN

Hoy día vivimos en una sociedad de consumo, donde el ideal de belleza que propugnan los medios de comunicación es la extrema delgadez y los métodos para mantenerse delgado y sano están comercializados, han cambiado radicalmente la concepción de sano y llega a ser un factor de riesgo para los trastornos de la conducta alimentaria.

Teniendo en cuenta los datos aportados de análisis con encuestas, nuestro principal objetivo es valorar la incidencia real que provoca los estereotipos en aparición de TCA en adolescentes de entre 13 y 17 años.

CONCLUSIONES

Los datos obtenidos en nuestro estudio, permiten interpretar que la insatisfacción corporal se presenta con más prevalencia en el género femenino que en el masculino, y confirman, en parte, los resultados de la literatura científica que se están publicando en los últimos años acerca del comportamiento del género sobre la imagen corporal. 

Poseer una satisfacción corporal alta disminuye el riesgo de padecer patologías de la conducta alimentaria por lo cual, a la vista de los resultados de este estudio, se deberá trabajar en ambos sexos, sobre todo en el género femenino sobre la autoestima personal como una de las estrategias preventivas. Atendiendo a los resultados más relevantes, obtenemos las siguientes conclusiones de acuerdo con nuestra hipótesis.

- Un 55,88% de los chicos nunca tienden a tener pensamientos depresivos debido a su apariencia física, contra un 44,22% de las chicas, lo que indica que ellas tienden a padecer más los efectos psicológicos que acarrea el ideal de belleza actual.

- De los adolescentes que indicaron que pensaban muy a menudo que debían perder peso, el 67% eran chicas mientras que solo un 33% eran chicos, esto nos vuelve a indicar que ellas sienten una presión social mayor a la vez que tienen una menor autoestima.

- Sobre los datos referentes a la importancia que le dan a la percepción que tenga la sociedad sobre su imagen corporal, vuelven a despuntar los resultados en el género femenino, volviendo a darle una puntuación de 0 el 62,5% de los niños y tan solo un 37,5% de las niñas.

Todo esto indica que por desgracia, en la actualidad, el ideal de belleza afecta de forma significativa al género femenino con respecto al género masculino, y que cada vez se tienen dichos “complejos” desde más jóvenes.

Sesiones Teóricas Estadística y TIC. Tema 9.

Estadística inferencial: Muestreo y estimación

La inferencia estadística es una parte de la estadística que comprende los métodos y procedimientos que por medio de la inducción determina propiedades de una población estadística, a partir de una pequeña parte de la misma (muestra). Durante la inferencia estadística siempre hay un error aleatorio y la inferencia estadística comprende:

• Al conjunto de pacientes sobre los que queremos estudiar alguna cuestión, población de estudio
• Al conjunto de individuos concretos que participan, muestra
• Al número de individuos e la muestra, tamaño muestral 
• Al conjunto de procedimientos que nos permite pasar de lo particular, a lo general, le denominamos inferencia estadística
• Al conjunto de procedimientos que permiten elegir muestras, técnicas de muestreo 

El error estándar, es la medida que trata de captar la variabilidad de los valores del estimador, mide el grado de variabilidad en los valores del estimador. Su cálculo depende de cada estimador.

Para una media el error estándar sería

Para una proporción

El cálculo de los intervalos de confianza son un medio de conocer el parámetro de una población midiendo el error que tienen que ver con el azar, son un par de valores entre los cuales podemos asegurar que el valor del parámetro es mayor o menos que ambos números. 

Explicaremos el cálculo del indice de confianza mediante un caso práctico.

• En un centro de salud se pretende realizar un estudio sobre tabaquismo, para lo que se selecciona una muestra de 337 pacientes. Los enfermeros del centro de salud encontraron que en total en la muestra había 83 fumadores habituales. Se pide que calculemos el intervalo de confianza al 95% (z=3) para la proporción de tabaquismo en el total de población del centro de salud.

I.C= estimador (proporción o media) +/- e x z

Como en este caso se trata de una proporción hallaremos la p, dividiendo el numero de casos que encontramos entre el total de la muestra, 83/337= 0,24. Como también nos falta el error aleatorio, lo calculamos, y lo multiplicamos por la Z.

El resultado nos da 0,284 y 0,196, por tanto en la población entre el 19,6 y el 28,4%, la población es fumadora con un indice de confianza del 95%.

TIPOS DE MUESTREO

Tamaño de la muestra.

El tamaño de la muestra a tomar va  a depender de:

•  Error estándar
•  De la mínima diferencia entre los grupos de comparación que se considera importante en los valores de la variable a estudiar. Más grande debe ser la muestra para que más pequeño sea el error.
• De la variabilidad de la variable a estudiar (varianza en la población).
• El tamaño de la población de estudio.

Para proporciones 

Para medias

Seminarios Estadística y TIC. Seminario 4.

Este seminario fue dedicado a resolver dudas que quedaron de la clase anterior, realizando problemas de Chi cuadrado para aclarar su resolución. Para proceder a su explicación pondremos el siguiente ejemplo.

1. A un grupo de enfermeros que se quejaban de que no dormían bien se les dio somníferos y placebos, obteniendo los siguientes datos.

Antes de continuar con la resolución del problema, procedemos a plantear las hipótesis necesarias, ya que Chi cuadrado se utiliza para saber si aceptamos o rechazamos la hipótesis nula.

• H0 no existe relación entre tomar somníferos o placebos para dormir bien.
• H1 tomar somníferos mejora el sueño.

Posteriormente procedemos a completar la tabla con los totales observados, y a realizar la tabla de datos esperados ante este estudio, que se calcularía multiplicando los totales parciales de cada opción entre el total de casos.

Una vez que realizamos todos lo valores para los datos esperados, introducimos los datos y realizaremos la fórmula de Chi cuadrado 

Llegados a este punto, solo nos queda calcular los grados de libertad que son el (Nº FILAS-1)(Nº COLUMNAS-1)= 1 y observar en la tabla de valores de Chi cuadrado, cual sería el valor que debería darnos para que p<0,05. En este caso, sería:

El valor observado en la tabla es de 3,84 mientras que nuestro valor calculado nos sale 2,57 como 2,57<3,84 aceptamos la hipótesis nula, es decir no hay relación entre tomar somníferos o placebos para conciliar mejor el sueño.

Seminarios Estadística y TIC. Seminario 3.

Durante el tercer seminario de la asignatura, y habiéndonos enseñado las nociones básicas sobre el programa EpiInfo durante el seminario dos, nos mostraron como hacer gráficos y cálculos, estadísticos utilizando de nuevo este programa, como diagramas de barras gráficos de sectores, calculo de Chi cuadrado, tablas de frecuencia...

Este seminario me resultó bastante útil ya que para nuestro trabajo final de investigación teníamos que realizar dichos cálculos y no sabíamos como hacerlo, aquí dejo unos ejemplos de los datos obtenidos en nuestro trabajo final, que logramos gracias a aprender a manejar este programa.

Sesiones Teóricas Estadística y TIC. Tema 8.

Medidas de tendencia central, posición y dispersión

Medidas de posición: dan idea de la magnitud, tamaño o posición de las observaciones de los datos.

Tendencia central: nos dan idea del comportamiento central de la muestra.

Medidas de dispersión: nos dan una idea acerca de la heterogeneidad de la muestra, es decir,  si está muy dispersa o no.

Medidas de tendencia central

• Media aritmética, es el centro geométrico o de gravedad de nuestros datos, siendo la suma de todos los valores de la variable observada entre el total de observaciones. Cuando se trata de datos agrupados la media se calcula de la siguiente manera:

• Mediana, es el valor de la observación por encima del cual el 50% de los datos son mayores y el otro 50% son menores. También corresponde a una medida de posición.
• Moda. es el valor que se repite con mayor frecuencia. Puede ser bimodal o multimodal si se repite más de un número. Si los datos están agrupados se habla de clase modal y corresponde a aquel intervalo en el que el coeficiente entre la frecuencia y la amplitud sea mayor.

Medidas de Posición

Los cuantiles se calculan para variables cuantitativas y al igual que la mediana, solo tienen en cuenta la posición de los valores en la muestra.

• Percentiles: Dividen la muestra en 100 partes, el percentil "I" es aquel en el que el I% de los valores se sitúan por debajo y el 100-I% se sitúa por encima.
• Deciles: Divide la muestra en 10 partes, el decil "i" es aquel en el que el I/10% de los valores son menores que él y el I-100/10% son mayores.
• Cuartiles: Son aquellos que dividen la muestra en 4, donde el Q1 se refiere al 25% y el Q4 al 100%.

P50 = D5 = Q2(50%) = MEDIANA

Medidas de dispersión

Asimetría y curtosis

• Asimetría: los resultados pueden ser los siguientes:
• g1=0 es simétrica, es decir, existe la misma concentración de valores a la derecha que a la izquierda de la media
• g1>0 asimétrica positiva, existiendo mayor concentración de valores a la derecha de la media
• g1<0 asimétrica negativa, existiendo mayor concentración de valores a la izquierda de la media.

• Curtosis: sirve para medir el grado de concentración de los valores de concentración que oma en torno a su media, mientras más se acumulen los datos, más apuntada será la curva.
• g2=0 mesocúrtica, siendo el grado de concentración medio 
• g2>0 leptocúrtica, elevado grado de concentración en torno a los valores centrales
• g2<0 platicúrtica, presentan un grado reducido de concentración alrededor de los valores centrales de la variable.

Sesiones teóricas Estadística y TIC. Tema 7

Introducción a la bioestadística 

La bioestadística es el cuerpo de conocimientos que se encarga de cuantificar la variabilidad.
Partimos de la base de que las variables son diferentes, por tanto habrá diferentes métodos de medición, utilizando diferentes escalas.

También tenemos diferentes tipos de variables en función de lo que estemos midiendo.

• Variables cualitativas: son aquellas que no pueden ser medidas, no se puede medir por ejemplo el estado civil o el sexo de la persona. 
• Dicotómicas: tienen dos niveles o categorías como por ejemplo el sexo (hombre o mujer)
• Policotómicas: tienen mas de dos categorías como puede ser el estado civil (soltero, casado, viudo...)
• Variables cuantitativas: son aquellas que pueden ser medidas, dentro de este tipo nos encontramos:
• Continuas: Adquieren una escala infinita de valores, pueden ser subdivididas como el peso.
• Discretas: solo pueden tomar un número finito de valores, como ocurre con el número de hijos.

REPRESENTACIÓN DE DATOS

- Diagrama de barras que se utiliza para la medición de variables cualitativas, nominales y sobre todo, policotómicas, existiendo variaciones como los pictogramas donde la barra es sustituida por iconos o imágenes que representen lo que estamos estudiando.

- Histograma y polígono de frecuencia para variables cualitativas. Para realizar esto, en primer lugar realizamos una tabla de frecuencia, que sigue los siguientes pasos:

1. Hallamos recorrido o rango, que es el valor mayor menos el menor,
2. Posteriormente hallaremos el número de intervalos haciendo la raíz cuadrada de n.
3. Por último para hallar la amplitud del intervalo dividiremos el Re entre la raíz cuadrada de n.

Sesiones teóricas Estadística y TIC. Tema 6.

Diseño, material y métodos.

Dentro del material y métodos nos encontramos con la población de estudio y el muestreo.

• La población de estudio es la selección de individuos en búsqueda de validez interna y externa, evitando a su vez los sesgos de selección etc.
• Muestreo, cuando no es posible incorporar toda la población de estudio. Se considerará entonces tanto el tamaño de la muestra como la representación del muestreo aleatorio simple.

Asignación del diseño de investigación en función de la pregunta de investigación.

MEDIDAS DE FRECUENCIA EN ESTUDIOS DESCRIPTIVOS

• Medida de prevalencia: Estudia la situación en un punto determinado en el tiempo. Describe en que proporción de la población está afectando el problema en un punto específico en el tiempo, por ejemplo el número de personas que padecen Diabetes Mellitus en 2015. Está medida es adimensional, es decir, no se puede medir y adquirirá valores del 0 al 1.

• Medidas de incidencia

Incidencia acumulada: calcula la proporción de incidencia, es decir, calcula el riesgo de que se produzca un fenómeno. También se puede definir como la proporción de sujetos que desarrollan la enfermedad en un periodo de tiempo, del totalde población de riesgo al inicio del periodo.

Tasa de incidencia: se refiere a la velocidad con la que aparecen los nuevos casos con respecto al tamaño de la población. Es necesario especificar la unidad de tiempo a la que nos referimos con la tasa, y puede obtener valores por encima de 1.

ESTUDIOS DE SEGUIMIENTO Y EXPERIMENTALES

Riesgo relativo: Es la relación entre la incidencia en expuestos y la incidencia en los no expuestos, cuando el riesgo relativo es 1, quiere decir que no hay relación entre las incidencias de expuestos y no expuestos, por lo que aceptamos la hipóteis nula.

ESTUDIOS DE CASOS Y CONTROLES

En este tipo de estudio se comparan dos grupos, uno que presenta la variable dependiente y otro grupo control que no la presenta. Se calculará la ODDS Ratio mediante:

• ODDS casos: Presencia del factor entre los casos/ ausencia del factor entre los casos
• ODDS controles: Presencia del factor entre los controles/ ausencia del factor entre los controles

Atendiendo a los valores que nos de ODDS ratio podemos, aceptar o no la hipótesis nula.

• Cuando ODSS ratio= 1 aceptaremos la hipótesis nula
• Cuando ODDS ratio > 1 los casos tienen mas riesgo de exposición al factor
• Cuando ODDS ratio < 1 los controles tienen mas riesgo de exposición al factor